Variabili Dummy and Dati Italiani

Variabili Dummy

Le variabili dummy sono utilizzate per analizzare variabili categoriche.

Dati sui lavoratori italiani

Utilizeremo un dataset contenente alcuni variabili che descrivono le caratteristiche di una campione di lavoratori dipendenti italiani.

Variabile	Descrizione
`retric`	Retribuzione mensile netta
`genere`	Genere del lavoratore
`regione`	Regione di residenza
`edulev`	Livello di istruzione
`istruzione_anni`	Anni di istruzione completati
`eta`	Età del lavoratore
`titolo10`	Titolo di studio
`detind`	Tipo di contratto di lavoro (indeterminato, determinato)
`piepar`	Tipo di orario di lavoro (pieno, parziale)
`tenure`	Anni di lavoro presso l’attuale datore di lavoro
`cittadinanza`	Se il lavoratore ha la cittadinanza italiana
`sg13`	Luogo di nascita
`orelav`	Ore di lavoro settimanali
`genere_dummy`	Variabile dummy per il genere (1 = Femmina, 0 = Maschio)

Il file può essere scaricato qua.

Salari per genere

Consideriamo la variabile genere:

head(df[, "genere"])

# A tibble: 6 × 1
  genere 
  <chr>  
1 Maschio
2 Femmina
3 Femmina
4 Maschio
5 Maschio
6 Femmina

La variabile assume il valore maschio o femmina a seconda che l’individua sia di genere maschile o femminile. Possiamo creare la variabile manualmente nel modo seguente

df <- df %>% mutate(Maschio = ifelse(genere=="Maschio", 1, 0))

La variabile Maschio prende il valore 1 se il genere dell’individuo è maschile e 0 altrimenti.

Possiamo utilizzare questa variabile per analizzare la variabile genere. Per esempio, possiamo prendere la media di Maschio

mean(df$Maschio)

[1] 0.5345987

La media nel caso di una variabile dummy è la percentuale di osservazioni che prendono il valore uno. Nel caso dei nostri dati, \(\bar{X}_{maschi}=0.535\) indica che circa il 53.46% dei lavoratori nel nostro campione è maschio.

Non c’è nulla di speciale nella scelta di “maschio” come valore per assegnare alla variabile dummy il valore 1. Possiamo infatti creare la variabile dummy Femmina con il valore 1 qualora il lavoratore sia di genere femminile.

df <- df %>% mutate(Femmina = ifelse(genere=="Femmina", 1, 0))

In questo caso, \(\bar{X}_{femmina}=0.465\) indica che circa il 46.54 dei lavoratori nel nostro campione è una donna (questa percentuale non è altro che \(1-\bar{X}_{maschio}\).)

Come possiamo usare questa variabile in una regressione? Possiamo usare la dummy come variabile indipendente.

lm_maschi <- feols(retric~Maschio, data = df)
lm_maschi

OLS estimation, Dep. Var.: retric
Observations: 138,618 
Standard-errors: IID 
            Estimate Std. Error t value  Pr(>|t|)    
(Intercept) 1171.258    1.99513 587.058 < 2.2e-16 ***
Maschio      281.449    2.72871 103.144 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 506.7   Adj. R2: 0.071272

L’interpretazione del coefficiente sulla dummy non è altro che la differenza dela salario fra uomini (Maschio=1) e donne (Maschio=0). Quindi, visto che \(\hat{\beta}_1 = 281.4492935\), gli uomini nel nostro campione guadagnano in media \(281.4492935\) euro piu’ delle donne. L’intercetta è in questa regressione la media (sempre nel campione) del salario delle donne (l’intercetta è interpretabile come la media della variabile dipendente quando i regressori sono uguali a zero).

Se utilizziamo la dummy Femmina invece della variabile dummy Maschio, i coefficienti stimati saranno diversi, ma la loro interpetazione finale sarà identica.

lm_femmine <- feols(retric~Femmina, data = df)
lm_femmine

OLS estimation, Dep. Var.: retric
Observations: 138,618 
Standard-errors: IID 
            Estimate Std. Error  t value  Pr(>|t|)    
(Intercept) 1452.708    1.86154  780.381 < 2.2e-16 ***
Femmina     -281.449    2.72871 -103.144 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 506.7   Adj. R2: 0.071272

In questa nuova regression, \(\hat{\beta}_1 = 1452.7076446\), e quindi possiamo dire che le donne nel nostro campione guadagnano in media \(1452.7076446\) euro in meno degli uomini. L’intercetta è invece la media del salario degli uomini.

Se calcolassimo le medie e la differenze delle medie manualemnte senza usare la regressione otterremo gli stessi risultati. Per esempio, il salario medio dei lavoratori di sesso maschile è esattamente uguale al coefficiente \(\hat{\beta}_0\) nella regressione che usa la veriaile dummy Femmina:

mean(df$retric[df$genere=="Maschio"])

[1] 1452.708

Per avere una completa panaromica della media di retric per genere possiamo usare la funzione group_by e summarize di dplyr”

df %>% group_by(genere) %>% summarize(mean(retric))

# A tibble: 2 × 2
  genere  `mean(retric)`
  <chr>            <dbl>
1 Femmina          1171.
2 Maschio          1453.

I coefficienti delle due regressioni stimano i corrispondenti valori della popolazione: \(\hat{\beta}_0\) stima la media nella popolazione dei salari per il caso in cui la variabile dummy è zero; \(\hat{\beta}_1\) stima la differenza dei salari medi nella poplazione fra i lavoratori con variabile dummy uguale a 1 e variabile dummy uguale a zero. Quindi possiamo chiederci se questa differenza nei salari che vediamo nel campioni è probabile che permangano qualora avessimo a disposizione l’intera popolazione. L’intervallo di confidenza risponde a questa domanda fornendoci un intervallo di valori probabili della differenza salariale fra uomini e donne nel campione:

confint(lm_maschi)

                2.5 %    97.5 %
(Intercept) 1167.3479 1175.1688
Maschio      276.1011  286.7975

Gli intervalli sono molto piccoli (come era prevedibile vista la grandezza del campione) e ci dice che questa differenza non è probabilmenmte dovuta al particolare compione che stiamo analizzando.

Salari per regione

Una variabile particolarmente interessante del nostro dataset è la variabile regione che fornisce la regione di residenza di ciascun lavoratore nel nostro campione

head(df[,"regione"])

# A tibble: 6 × 1
  regione  
  <chr>    
1 Puglia   
2 Lombardia
3 Piemonte 
4 Lombardia
5 Umbria   
6 Campania

L’esistenza di differenza salariali nelle regioni italiane può essere investigata mediante un grafico che mostra la distribuzione di retric per ciascuna regione:

ggplot(df, aes(x = retric)) + 
  xlab("Regione") + 
  ylab("Retribuzione netta") +
  geom_histogram(aes(y=stat(density)))  + 
  theme_minimal() + 
  theme(axis.text.x = 
          element_text(
            angle = 25,
            vjust = 0.5,
            hjust = 1,
            size = 6), 
        axis.text.y = 
          element_text(size = 6)
        ) + facet_wrap(~regione)

Warning: `stat(density)` was deprecated in ggplot2 3.4.0.
ℹ Please use `after_stat(density)` instead.

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.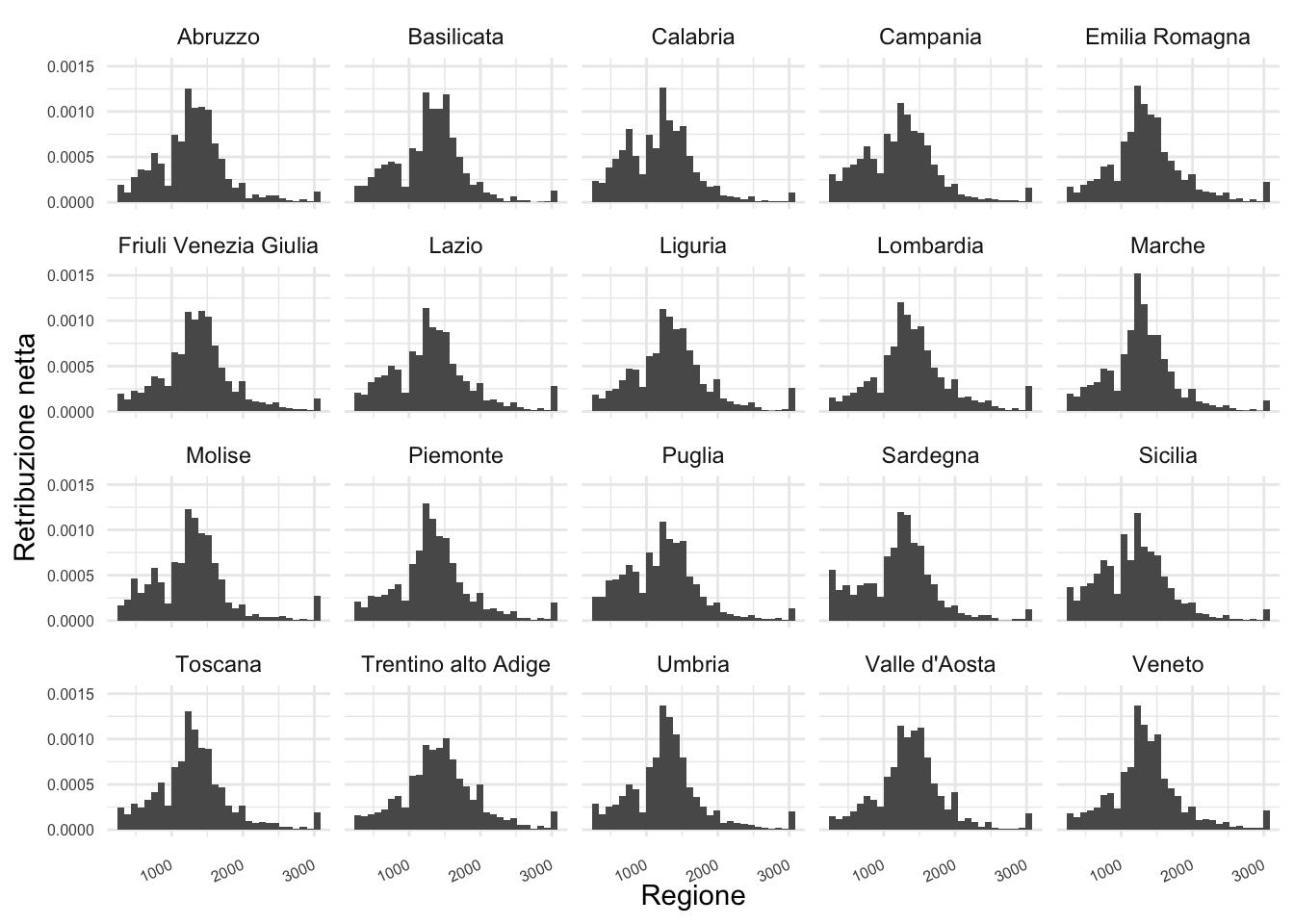

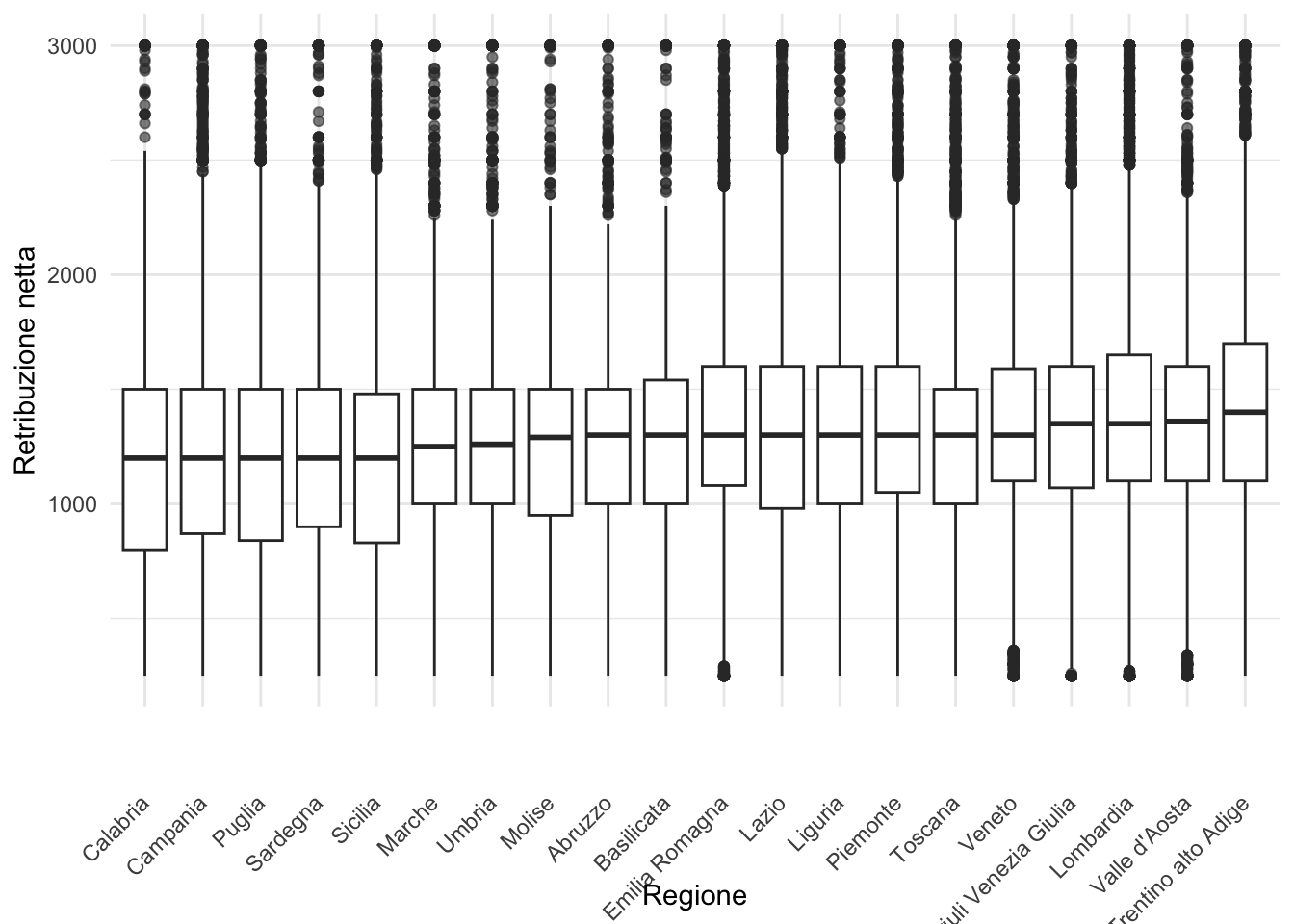
ggplot(df, aes(y = retric, x = fct_reorder(regione, retric))) + 
  xlab("Regione") + 
  ylab("Retribuzione netta") +
  geom_boxplot(outlier.alpha = 0.6)  + 
  theme_minimal() + 
  theme(axis.text.x = element_text(
  angle = 45,
  vjust = 0.5,
  hjust = 1
))

Pur essendo una variabile categorica, regione prende piu’ di due valori e quindi non è possibile codificare l’informazione contenuta in essa mediante un’unica variabile dummy. In questo caso creiama una dummy per ciascuna regione: una dummy Lombardia che prende il valore 1 per quei lavoratori che risiedono in Lombardia e 0 per gli altri, una dummy Sicilia per i lavoratori che risiedono in Sicilia e 0 per gli altri, e così via.

E’ possibile creare queste dummy manualmente:

df <- df %>% mutate(Lombardia = ifelse(regione=="Lombardia", 1, 0),
                    Sicilia = ifelse(regione=="Sicilia", 1, 0),
                    .
                    .
                    )

La creazione manuale è però tediosa e prona ad errori. È preferibile automatizzare il processo di creazione delle dummy mediante il pachetto fastDummies.

library(fastDummies)
df <- fastDummies::dummy_cols(df, select_columns = "regione", 
                              omit_colname_prefix = TRUE)

Dopo l’esecuzione del codice, df conterrà una variabile dummy per ciascuna regione. Possiamo adesso calcolare la media di ciascuna dummy così creata per ottenere la percentuale dei residenti in ciascuna regione. Per esempio,

mean(df$Calabria)

[1] 0.01961506

indica che circa il 1.96% dei lavoratori del nostro campione è residente in Calabria.

Qual è l’interpretazione della regressione in cui aggiungiamo tutte le dummy?

lm_regione <- feols(retric~Abruzzo+Basilicata+ Calabria + Campania + 
`Emilia Romagna` + `Friuli Venezia Giulia` + 
Lazio + Liguria + Lombardia + Marche + Molise+
Piemonte + Puglia + Sardegna + Sicilia +
Toscana + `Trentino alto Adige` + Umbria + 
`Valle d'Aosta` + Veneto, data = df)

The variable 'Veneto' has been removed because of collinearity (see $collin.var).

summary(lm_regione)

OLS estimation, Dep. Var.: retric
Observations: 138,618 
Standard-errors: IID 
                          Estimate Std. Error    t value   Pr(>|t|)    
(Intercept)             1352.67843    5.88778 229.743479  < 2.2e-16 ***
Abruzzo                  -67.03866   11.67738  -5.740897 9.4372e-09 ***
Basilicata               -62.22983   10.73230  -5.798367 6.7108e-09 ***
Calabria                -159.50447   11.59058 -13.761558  < 2.2e-16 ***
Campania                -124.70487    8.18131 -15.242653  < 2.2e-16 ***
`Emilia Romagna`           8.80117    7.58301   1.160645 2.4579e-01    
`Friuli Venezia Giulia`    3.25957    9.44556   0.345090 7.3003e-01    
Lazio                    -30.97062    7.82437  -3.958227 7.5546e-05 ***
Liguria                   -2.50250   10.18666  -0.245665 8.0594e-01    
Lombardia                 56.13623    6.91684   8.115883 4.8617e-16 ***
Marche                   -76.95157   10.14049  -7.588549 3.2551e-14 ***
Molise                   -79.67389   14.50991  -5.490998 4.0037e-08 ***
Piemonte                 -12.44023    7.66513  -1.622964 1.0460e-01    
Puglia                  -139.24116    9.10816 -15.287521  < 2.2e-16 ***
Sardegna                -150.99941   10.57937 -14.273005  < 2.2e-16 ***
Sicilia                 -166.02165    7.95915 -20.859208  < 2.2e-16 ***
Toscana                  -54.75509    8.10400  -6.756549 1.4187e-11 ***
`Trentino alto Adige`     81.81903    7.95858  10.280604  < 2.2e-16 ***
Umbria                   -79.82247   10.44123  -7.644928 2.1040e-14 ***
`Valle d'Aosta`           14.82207    9.45899   1.566983 1.1712e-01    
... 1 variable was removed because of collinearity (Veneto)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 520.6   Adj. R2: 0.019842

La funzione feols ci informa che una delle variabili dummy è stata rimossa per evitare la collinearità (la trappola delle variabili dummy). I coefficienti della regressione sono la differenza fra il salario medio nella regione a cui il coefficiente si riferisce e la regione omessa dalla regressione che, in questo caso, è la regione Veneto. Per esempio, il coefficite della dummy Sicilia ci dice che in media i lavoratori residenti nell’isola guadagnano 166.0216453 euro in meno dei lavoratori residenti in Veneto.

Aggiungere variabili dummy al modello di regressione è un’operazione così frequente che R possiede un meccanismo automatico per la loro gestione: aggiungere nella regressione la variabile categorica automaticamente crea e aggiunge al modello una dummy per ciascuna categoria.

feols(retric~regione, data=df)

OLS estimation, Dep. Var.: retric
Observations: 138,618 
Standard-errors: IID 
                               Estimate Std. Error    t value   Pr(>|t|)    
(Intercept)                  1285.63977    10.0844 127.487822  < 2.2e-16 ***
regioneBasilicata               4.80883    13.4986   0.356247 7.2166e-01    
regioneCalabria               -92.46581    14.1905  -6.516024 7.2442e-11 ***
regioneCampania               -57.66621    11.5743  -4.982284 6.2913e-07 ***
regioneEmilia Romagna          75.83983    11.1594   6.796071 1.0794e-11 ***
regioneFriuli Venezia Giulia   70.29823    12.4999   5.623892 1.8706e-08 ***
regioneLazio                   36.06804    11.3248   3.184884 1.4484e-03 ** 
regioneLiguria                 64.53616    13.0689   4.938129 7.8967e-07 ***
... 12 coefficients remaining (display them with summary() or use argument n)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 520.6   Adj. R2: 0.019842

Se volessimo ottenere i risultati delle regressione omettando un’altra regione, possiamo usare la funzione i() che prende come pri argomento la variabile categorica e come secondo argomento la categoria da escludere. Pertanto, per escludere la dummy riferita alla regione Campania usiamo come regressore i(regione, "Campanio").

feols(retric~i(regione, "Campania"), data=df)

OLS estimation, Dep. Var.: retric
Observations: 138,618 
Standard-errors: IID 
                                Estimate Std. Error   t value   Pr(>|t|)    
(Intercept)                    1227.9736    5.68048 216.17407  < 2.2e-16 ***
regione::Abruzzo                 57.6662   11.57425   4.98228 6.2913e-07 ***
regione::Basilicata              62.4750   10.62000   5.88277 4.0437e-09 ***
regione::Calabria               -34.7996   11.48667  -3.02956 2.4495e-03 ** 
regione::Emilia Romagna         133.5060    7.42320  17.98496  < 2.2e-16 ***
regione::Friuli Venezia Giulia  127.9644    9.31776  13.73339  < 2.2e-16 ***
regione::Lazio                   93.7343    7.66960  12.22154  < 2.2e-16 ***
regione::Liguria                122.2024   10.06826  12.13738  < 2.2e-16 ***
... 12 coefficients remaining (display them with summary() or use argument n)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 520.6   Adj. R2: 0.019842

Come nel caso della variabile genere, i valori dei coefficienti sono esattamenti uguali alle differenze delle medie calcolate manualmente. Per convincerci di ciò, possiamo calcolare la media di retric per regione e sottrarre la media della Campania usando la funzione group_by e summarize di dplyr.

## Calcoliamo la media dei salari in Campania
mc <- df %>% filter(regione=="Campania") %>% 
  summarize(mc = mean(retric)) %>% pull(mc)
## `mc` e' uguale all'intercetta della regressione che 
## esclude la dummy per la Campania.
## Calcoliamo la media dei salari in ciascuna regione e sottraiamo
## `mc`
df %>% filter(regione!="Campania") %>% 
  group_by(regione) %>% 
  summarize(`Differenza da media Campania` = mean(retric)-mc) %>%
  arrange(`Differenza da media Campania`)

# A tibble: 19 × 2
   regione               `Differenza da media Campania`
   <chr>                                          <dbl>
 1 Sicilia                                        -41.3
 2 Calabria                                       -34.8
 3 Sardegna                                       -26.3
 4 Puglia                                         -14.5
 5 Umbria                                          44.9
 6 Molise                                          45.0
 7 Marche                                          47.8
 8 Abruzzo                                         57.7
 9 Basilicata                                      62.5
10 Toscana                                         69.9
11 Lazio                                           93.7
12 Piemonte                                       112. 
13 Liguria                                        122. 
14 Veneto                                         125. 
15 Friuli Venezia Giulia                          128. 
16 Emilia Romagna                                 134. 
17 Valle d'Aosta                                  140. 
18 Lombardia                                      181. 
19 Trentino alto Adige                            207.

Il vantaggio di usare la regressione rispetto a calcolare la differenza medie manualmente è la regressione ci restituisce gli errori standard delle differenze delle media consentendoci la costruzione immediata degli intervalli di confidenza.

confint(lm_regione)

                              2.5 %      97.5 %
(Intercept)             1341.138502 1364.218367
Abruzzo                  -89.926111  -44.151208
Basilicata               -83.264940  -41.194721
Calabria                -182.221796 -136.787151
Campania                -140.740079 -108.669653
`Emilia Romagna`          -6.061372   23.663721
`Friuli Venezia Giulia`  -15.253560   21.772697
Lazio                    -46.306226  -15.635005
Liguria                  -22.468156   17.463149
Lombardia                 42.579363   69.693096
Marche                   -96.826733  -57.076413
Molise                  -108.113045  -51.234739
Piemonte                 -27.463752    2.583285
Puglia                  -157.092974 -121.389340
Sardegna                -171.734783 -130.264047
Sicilia                 -181.621436 -150.421854
Toscana                  -70.638786  -38.871401
`Trentino alto Adige`     66.220357   97.417696
Umbria                  -100.287085  -59.357850
`Valle d'Aosta`           -3.717364   33.361506

Gender gap

L’obiettivo è misurare la differenza salariale tra donne e uomini che condividono le stesse caratteristiche rilevanti, come l’istruzione, l’esperienza lavorativa, il settore di impiego, ecc., ma differiscono per genere.

lm_gp <- feols(retric~genere+regione, data=df)
lm_gp

OLS estimation, Dep. Var.: retric
Observations: 138,618 
Standard-errors: IID 
                                Estimate Std. Error    t value   Pr(>|t|)    
(Intercept)                  1118.134158    9.81249 113.950063  < 2.2e-16 ***
genereMaschio                 290.437520    2.70004 107.568035  < 2.2e-16 ***
regioneBasilicata               0.001989   12.96823   0.000153 9.9988e-01    
regioneCalabria               -91.809556   13.63291  -6.734407 1.6524e-11 ***
regioneCampania               -65.965371   11.11971  -5.932295 2.9944e-09 ***
regioneEmilia Romagna          95.899709   10.72248   8.943802  < 2.2e-16 ***
regioneFriuli Venezia Giulia   86.855842   12.00973   7.232126 4.7793e-13 ***
regioneLazio                   48.195564   10.88033   4.429603 9.4479e-06 ***
... 13 coefficients remaining (display them with summary() or use argument n)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 500.1   Adj. R2: 0.095359

In questa prima regressione stiamo “controllando” per la regione di residenza. L’interpretazione del coefficiente di gender è quindi la differenza media dei salari fra uomini e donne a parità di regione di residenza. La stima di tale differenza è di circa 290.44 euro. Questa differenza è statisticamente significativa, cioè possiamo rigettare l’ipotesi nulla che nella popolazione la differenza è uguale a zero (\(H_0: \beta_1=0\)) poichè l’intervallo di onfidenza non contiene zero o, equivalentemente, la statistica \(t\) è maggiore in valore assoluto del valore critico (\(1.96\)).

Chiaramente, uomini e donne possono differire per livelli di istruzione (istruzione_anno), per la tipologia di contratto (detind) e se lavorano in part-time (piepar) e per il numero di ore lavorate.

lm_gp2 <- feols(retric~istruzione_anni+piepar+detind+genere+regione, data=df)
lm_gp2

OLS estimation, Dep. Var.: retric
Observations: 138,618 
Standard-errors: IID 
                            Estimate Std. Error    t value   Pr(>|t|)    
(Intercept)               -19.714271   8.840365  -2.230029 2.5747e-02 *  
istruzione_anni            41.355406   0.261081 158.400638  < 2.2e-16 ***
piepartempo pieno         521.552688   2.792073 186.797681  < 2.2e-16 ***
detindtempo indeterminato 286.402687   2.939087  97.446140  < 2.2e-16 ***
genereMaschio             201.536591   2.283682  88.250741  < 2.2e-16 ***
regioneBasilicata          -0.101848  10.224505  -0.009961 9.9205e-01    
regioneCalabria           -39.440407  10.749966  -3.668887 2.4370e-04 ***
regioneCampania           -42.821891   8.767499  -4.884163 1.0398e-06 ***
... 16 coefficients remaining (display them with summary() or use argument n)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 394.3   Adj. R2: 0.437681

Per tenere conto delle ore lavorate (orelav) possiamo usare come variabile dipendente il rapporto fra il salario orario netto mensile e le ore lavorete nel mese (che è uguale a \(4\times orelav\)):

lm_gp3 <- feols(I(retric/(4*orelav))~istruzione_anni+piepar+detind+genere+regione, data=df)
lm_gp3

OLS estimation, Dep. Var.: I(retric/(4 * orelav))
Observations: 138,618 
Standard-errors: IID 
                           Estimate Std. Error   t value   Pr(>|t|)    
(Intercept)                3.724961   0.201074 18.525280  < 2.2e-16 ***
istruzione_anni            0.403373   0.005938 67.927402  < 2.2e-16 ***
piepartempo pieno         -0.178177   0.063506 -2.805674 5.0218e-03 ** 
detindtempo indeterminato  1.799457   0.066850 26.917971  < 2.2e-16 ***
genereMaschio              0.287500   0.051942  5.534970 3.1184e-08 ***
regioneBasilicata         -0.158508   0.232557 -0.681588 4.9550e-01    
regioneCalabria           -0.462131   0.244508 -1.890040 5.8755e-02 .  
regioneCampania           -0.312879   0.199417 -1.568968 1.1666e-01    
... 16 coefficients remaining (display them with summary() or use argument n)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 8.96792   Adj. R2: 0.040316

Esercizi:

Come possiamo interpretare il coefficiente su genereMaschio nell’ultima regressione? Per esempio, come è possibile interpretare la grandezza del coefficiente in maniera percentuale (per esemptio, di quanto è più alto il salario degli uomini in termini percentuali rispetto a quello delle donne?)
La differenza fra i salari fra uomini e donne nell’ultima regression è statisticamente significativa?
Quali sono le altre variabili che è probabile possono influenzare l’interpretezione del coefficiente su genereMaschio come indicativo di discriminazione?