# Installa il pacchetto ggplot2
install.packages("ggplot2")
# Carica il pacchetto ggplot2
library(ggplot2)R: Introduzione
Storia
R è un linguaggio di programmazione open source utilizzato per l’analisi e visualizzazione dei dati.
R è la versione open source di S, software sviluppato da John Chambers, Rick Becker and Allan Wilks presso i Bell Laboratories di AT&T alla fine degli anni ’70. Nell’idea del suoi creatori, S doveva essere un linguaggio di programmazione che fosse più semplice e più interattivo rispetto ai linguaggi utilizzati per l’analisi dei dati dell’epoca (FORTRAN e SAS).
R fu sviluppato inizialmente da Ross Ihaka e Robert Gentleman presso l’Università di Auckland, in Nuova Zelanda. La prima versione di R venne condivisa dai sui creatori nel 1993. Nel 1995 il software fu rilasciato sotto la licenza open source GNU GPL.
La versione 1.0 è stata rilasciata il 29 febbraio 2000 e da quel momento la crescita della sua popolarità non si è arrestata.
Negli ultimi dieci anni, due aziende hanno contribuito alla crescita di R: R Studio (oggi diventata Posit) e Revolution Analytics.
Revolution Analytics fondata nel 2007, è stata una delle prime società a offrire una versione commerciale di R. Revolution Analytics ha introdotto nuove funzionalità, come l’elaborazione parallela e distribuita, che hanno permesso di elaborare grandi quantità di dati in modo più efficiente. L’acquisizione di Revolution Analytics da parte di Microsoft nel 2015 ha ulteriormente rafforzato l’adozione di R, poiché Microsoft ha iniziato a integrare R in molti dei suoi prodotti, come SQL Server e Power BI.
RStudio, dal 2022 Posit, ha avuto un ruolo fondamentale nello sviluppo dell’ecosistema R. Fondata nel 2011 da JJ Allaire, l’azienda ha introdotto un ambiente di sviluppo integrato (IDE) che ha rivoluzionato l’interazione con il linguaggio e ha reso la programmazione in R più accessibile e intuitiva, facilitando la scrittura, il debug e la gestione dei pacchetti.
Oltre al suo IDE, RStudio ha svolto un ruolo chiave nello sviluppo del tidyverse, una collezione di pacchetti ideata e sviluppata da Hadley Wickham, uno dei più influenti progammatori di R e Chief Scientist di Posit. Il tidyverse comprende pacchetti come ggplot2, dplyr e tidyr usati per la visualizzazione, la manipolazione e la ristrutturazione dei dati. Questi strumenti hanno reso più efficiente e meno soggette a errori l’analisi dei dati promuovendo uno stile di programmazione coerente e leggibile.
R è oggi uno dei linguaggi di programmazione più popolari per l’analisi dei dati e la statistica negli ultimi anni. Ecco alcuni dati sull’adozione di R:
Numero di utenti: Secondo un sondaggio del 2022 condotto da Stack Overflow
Rè uno dei linguaggi di programmazione più popolare al mondo, utilizzato dal 4.7% degli sviluppatori ed è il primo fra i software specificatamente pensati per applicazioni statistiche.Numero di pacchetti: Il Comprehensive R Archive Network (CRAN), il principale repository di pacchetti per R, contiene oltre 19.000 pacchetti. Questi pacchetti coprono una vasta gamma di applicazioni che vanno dalla statistica al machine learning, dalla visualizzazione e manipolazione dei dati alla stesura automatica di report, e altri task generici non necessariamente legati alle applicazioni di carattere statistico.
Uso aziendale: L’adozione di
Rnell’ambiente aziendale è in costante aumento.
Installazione di R e Rstudio
R può essere scaricato gratuitamente dal sito ufficiale (www.r-project.org/) scegliendo la versione adatta al sistema operativo utilizzato.
Per installare RStudio sul tuo computer bisogna visitare https://posit.co/download/rstudio-desktop/, scaricare la versione di RStudio Desktop compatibile con il sistema operativo e seguire le istruzioni per completare l’installazione.
Una differenza chiave da comprendere capire è quella tra R, il linguaggio di programmazione mentre RStudio è un’interfaccia ad R che consente di lavorare maggiore facilità con R.
Calcoli di Base
R come una semplice calcolatrice.
Addizione, Sottrazione, Moltiplicazione e Divisione
| Matematica | Codice R |
Risultato |
|---|---|---|
| \(3 + 2\) | 3 + 2 |
5 |
| \(3 - 2\) | 3 - 2 |
1 |
| \(3 \cdot2\) | 3 * 2 |
6 |
| \(3 / 2\) | 3 / 2 |
1.5 |
Esponenti
| Matematica | Codice R |
Risultato |
|---|---|---|
| \(3^2\) | 3 ^ 2 |
9 |
| \(2^{(-3)}\) | 2 ^ (-3) |
0.125 |
| \(100^{1/2}\) | 100 ^ (1 / 2) |
10 |
| \(\sqrt{100}\) | sqrt(100) |
10 |
Costanti Matematiche
| Matematica | Codice R |
Risultato |
|---|---|---|
| \(\pi\) | pi |
3.1415927 |
| \(e\) | exp(1) |
2.7182818 |
Logaritmi
Nota che useremo \(\ln\) e \(\log\) in modo interscambiabile per indicare il logaritmo naturale. Non c’è ln() in R, invece usa log() per indicare il logaritmo naturale.
| Matematica | Codice R |
Risultato |
|---|---|---|
| \(\log(e)\) | log(exp(1)) |
1 |
| \(\log_{10}(1000)\) | log10(1000) |
3 |
| \(\log_{2}(8)\) | log2(8) |
3 |
| \(\log_{4}(16)\) | log(16, base = 4) |
2 |
Trigonometria
| Matematica | Codice R |
Risultato |
|---|---|---|
| \(\sin(\pi / 2)\) | sin(pi / 2) |
1 |
| \(\cos(0)\) | cos(0) |
1 |
I pacchetti di R
I pacchetti in R sono collezioni di funzioni, dati e codice compilato che sono sviluppati da terzi per aumentare le funzionalità di R. Sono fondamentali poiché permettono agli utenti di eseguire una vasta gamma di analisi e processi senza dover scrivere tanto codice. Ci sono migliaia di pacchetti disponibili su CRAN (Comprehensive R Archive Network), oltre a quelli disponibili su altre fonti come GitHub.
Per installare un pacchetto in R, si utilizza la funzione install.packages(). Questa funzione scarica e installa il pacchetto desiderato dal repository CRAN. Una volta installato un pacchetto, è necessario caricarlo nella sessione di lavoro corrente usando la funzione library() per poter utilizzare le sue funzionalità.
Ecco un esempio di come installare e caricare il pacchetto ggplot2:
In questo esempio, il primo comando installa ggplot2 e il secondo comando lo carica nella sessione di R attuale, rendendo disponibili tutte le sue funzioni e capacità.
I pacchetti possono anche essere installati da Rstudio, dal menu Strumenti|Installa pacchetti. Similarmente, i pacchetti possono essere aggiornati usando la voce Aggiorna pacchetti.
Alcuni pacchetti di R includono raccolte di dati (dataset). Questi dataset sono particolarmente utili. Per esempio, wooldridge, Ecdat e AER contengono vari dataset di carattere economico.
Per accedere ai dataset inclusi nei pacchetti bisogna installarli e poi caricarli.
# Installa il pacchetto AER
install.packages("AER")
# Installa il pacchetto wooldridge
install.packages("wooldridge")
# Carichiamo i pacchetti
library(AER)
library(wooldridge)
# Carica un dataset specifico, ad esempio 'Accident'
data(Fatalities)Alternativamente, i pacchetti possono essere installati direttamente da RStudio usando il menu Tools (Strumenti).
Dopo aver installato e caricato Ecdat il comando data() consente di caricare uso specifico dataset in memoria per essere poi utilizzato nella nostra sessione.
I dataset inclusi nei pacchetti offrono diversi vantaggi:
- Facilità di Accesso: Gli utenti possono accedere rapidamente a un’ampia gamma di dati senza doverli cercare o scaricare da fonti esterne.
- Validità e Affidabilità: I dati forniti nei pacchetti R sono generalmente ben documentati e validati, il che li rende affidabili per analisi e apprendimento.
Caricamento dei pacchetti
L’installazione rende disponibili i pacchetti sul proprio computer. Perché R possa utilizzare le funzionalità del pacchetto è necessario caricare i pacchetti utilizzando il comando library(). Ad esempio, per caricare il pacchetto Ecdat bisogna eseguire il seguente comando nella console R:
library(AER)I dataset di Ecdat
Per avere un’idea dei dataset messi a disposizione da Ecdat possiamo utilizzare la funzione di help
help(package="AER")I dataset possono essere caricati nella sessione di R mediante il comando data(). Per esempio, il seguente comando
data(CASchools)rende disponibile il dataset Caschool. Il data set può essere richiamato semplicemente digitando il suo nome
summary(CASchools) district school county grades
Length:420 Length:420 Sonoma : 29 KK-06: 61
Class :character Class :character Kern : 27 KK-08:359
Mode :character Mode :character Los Angeles: 27
Tulare : 24
San Diego : 21
Santa Clara: 20
(Other) :272
students teachers calworks lunch
Min. : 81.0 Min. : 4.85 Min. : 0.000 Min. : 0.00
1st Qu.: 379.0 1st Qu.: 19.66 1st Qu.: 4.395 1st Qu.: 23.28
Median : 950.5 Median : 48.56 Median :10.520 Median : 41.75
Mean : 2628.8 Mean : 129.07 Mean :13.246 Mean : 44.71
3rd Qu.: 3008.0 3rd Qu.: 146.35 3rd Qu.:18.981 3rd Qu.: 66.86
Max. :27176.0 Max. :1429.00 Max. :78.994 Max. :100.00
computer expenditure income english
Min. : 0.0 Min. :3926 Min. : 5.335 Min. : 0.000
1st Qu.: 46.0 1st Qu.:4906 1st Qu.:10.639 1st Qu.: 1.941
Median : 117.5 Median :5215 Median :13.728 Median : 8.778
Mean : 303.4 Mean :5312 Mean :15.317 Mean :15.768
3rd Qu.: 375.2 3rd Qu.:5601 3rd Qu.:17.629 3rd Qu.:22.970
Max. :3324.0 Max. :7712 Max. :55.328 Max. :85.540
read math
Min. :604.5 Min. :605.4
1st Qu.:640.4 1st Qu.:639.4
Median :655.8 Median :652.5
Mean :655.0 Mean :653.3
3rd Qu.:668.7 3rd Qu.:665.9
Max. :704.0 Max. :709.5
Il sistema di help
Il sistema di help di R è un’importante risorsa per gli utenti che utilizzano questo software. Consente di accedere a informazioni dettagliate su tutte le funzioni e i pacchetti di R, nonché di comprendere meglio il funzionamento del linguaggio di programmazione R.
Ogni funzione in R ha la sua pagina di help alla quale si può accedere tramite la funzione help() o tramite il simbolo ? seguito dal nome della funzione della quale si vogliono ottenee inforrmazioni. Per esempio
help(mean)apre la pagina di help relativa alla funzione mean.
La pagina di help fornisce una descrizione della funzione, i suoi argomenti e tipologia dei valori che la funzione restituisce. La maggior parte delle funzioni in R hanno esempi di utilizzo nella loro pagina di help.
Per ottenere aiuto sulle funzionalità di un pacchetto bisogna passare l’argomento packages seguito dal nome del pacchetto. Per esempio, il seguente comando mostra la pagina di help per il pacchetto ggplot2
help(packages="ggplot2")Primi grafici con ggplot2
I passi per ottenere un grafico con ggplot2 sono:
Installare e caricare il pacchetto
ggplot2utilizzando il comandoinstall.packages("ggplot2")seguito dalibrary(ggplot2).Caricare i dati che si desidera visualizzare in un data frame.
Creare un oggetto
ggplotutilizzando la funzioneggplot(). Gli argomenti di questa funzione sono ildata.framee la funzioneaesmediante la quale possono essere specificate le variabili che si desidera utilizzare per l’asse x e l’asse y.Aggiungere i livelli e gli stili al grafico utilizzando una serie di geometrie come
geom_point(),geom_line(),geom_bar(). Queste funzioni definiscono le modalità di rappresentazione dei dati nel grafico (ad esempio, con punti, linee, barre, ecc.).Aggiungere etichette, titoli e altre personalizzazioni utilizzando funzioni come
labs(),xlab(),ylab(),ggtitle()e altre funzioni di personalizzazione.
Ecco un esempio di codice di base per creare un grafico a dispersione utilizzando ggplot2:
library(ggplot2)
# Caricare i dati
data(CASchools)
## Creiamo le variabili
library(dplyr)
Attaching package: 'dplyr'The following object is masked from 'package:car':
recodeThe following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionCASchools <- CASchools |> mutate(str=students/teachers, testscr=(read+math)/2)
# Creare l'oggetto ggplot
scatterplot <- ggplot(CASchools, aes(x = str, y = testscr))
# Aggiungere i punti al grafico
scatterplot <- scatterplot + geom_point(col = "darkgreen")
# Aggiungere etichette e titoli
scatterplot <- scatterplot +
labs(title = "Grafico a dispersione - testscr/str",
x = "Rapporto studenti insegnanti", y = "Punteggi nei test")
# Visualizzare il grafico
scatterplot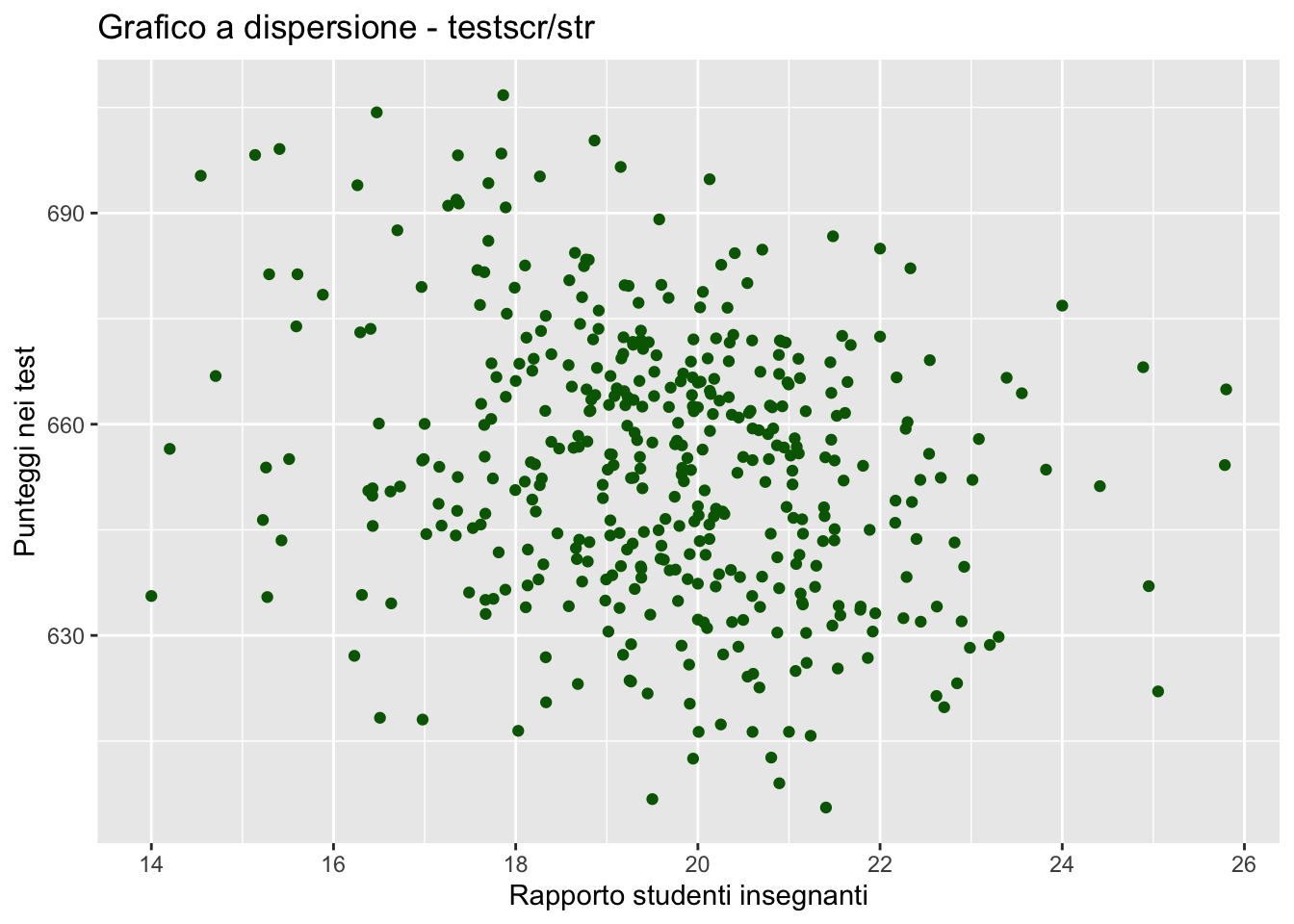
Questo è solo un esempio molto semplice, ma ggplot2 offre molte altre funzionalità per la creazione di grafici avanzati e personalizzati. Per esempio, possiamo cambiare il tema grafico usando theme_bw() che elimina i colori
scatterplot <- scatterplot + theme_bw()
scatterplot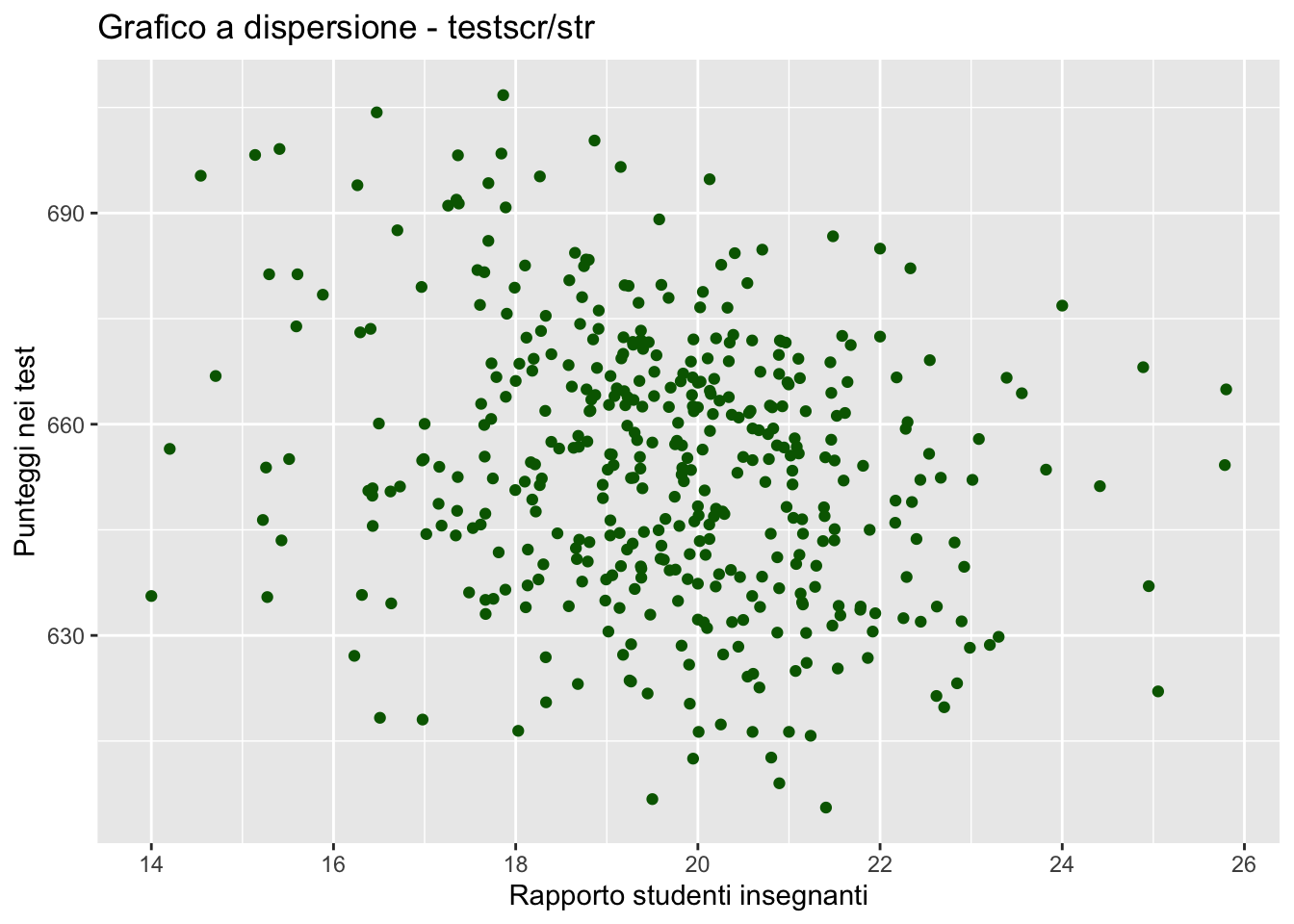
Possiamo anche costruire grafici raggruppati per variabile. Per ottenere un grafico a dispersione per str e testscr per le due tipologie di scuole grades=="KK-06" egrades=“KK-08”`:
scatterplot <- scatterplot + facet_wrap(~grades)
scatterplot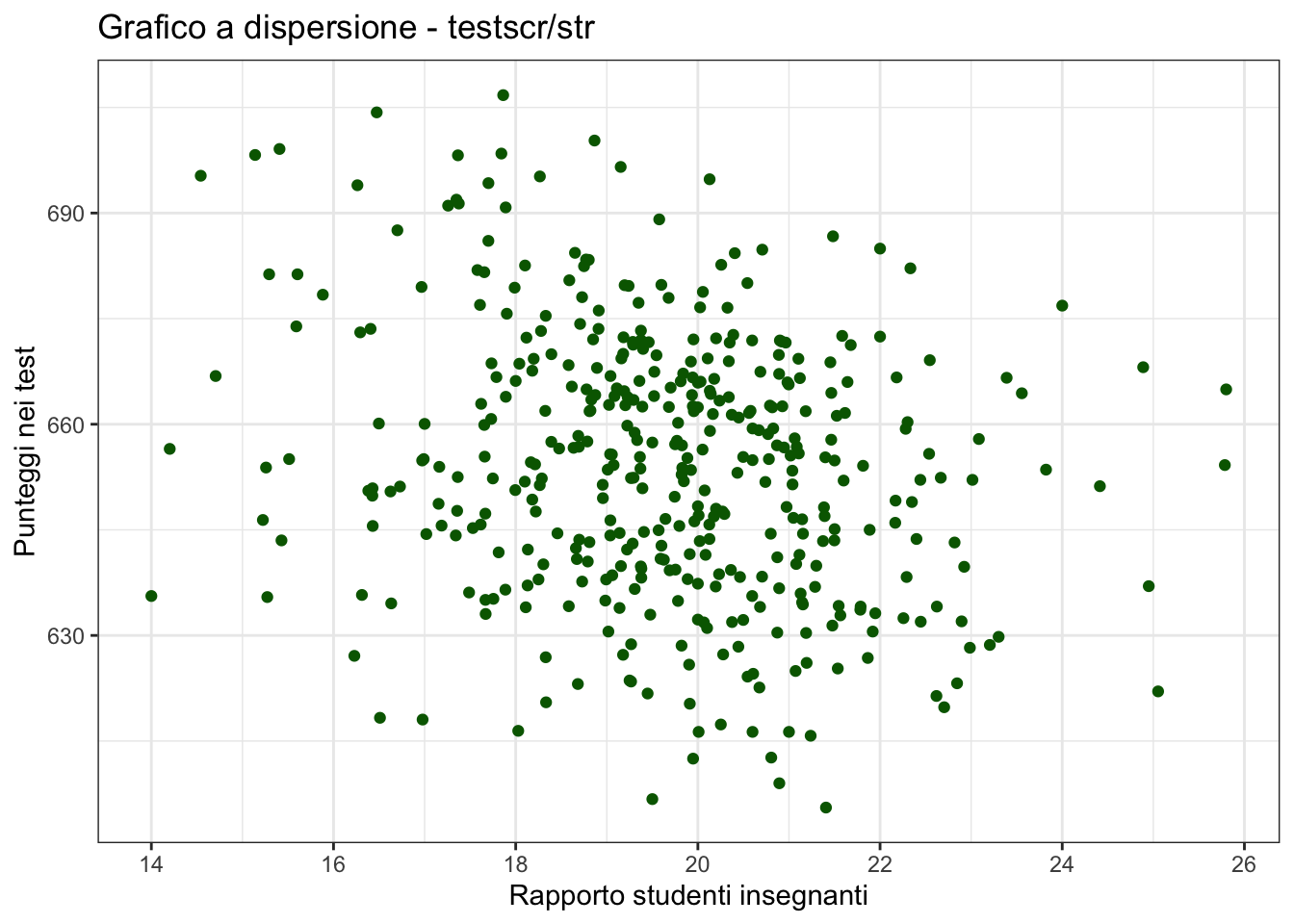
La funzione facet_wrap() in ggplot2 è utilizzata per dividere i dati in sottoinsiemi basati su una variabile e creare una griglia di grafici separati, ognuno dei quali visualizza i dati per uno dei livelli della variabile.
La sintassi di base di facet_wrap() è la seguente:
facet_wrap(~variable, nrow = x, ncol = y)Dove variable è la variabile che si vuole utilizzare per suddividere i dati in sottoinsiemi (nell precedente esempio abbiamo utilizzato grspan) e nrow e ncol specificano il numero di righe e colonne della griglia di grafici che si desidera creare.
Possiamo anche aggiungere le rette di regression a ciascun grafico usando la geometria geom_smooth
scatterplot + geom_smooth(method="lm", col = "darkred")`geom_smooth()` using formula = 'y ~ x'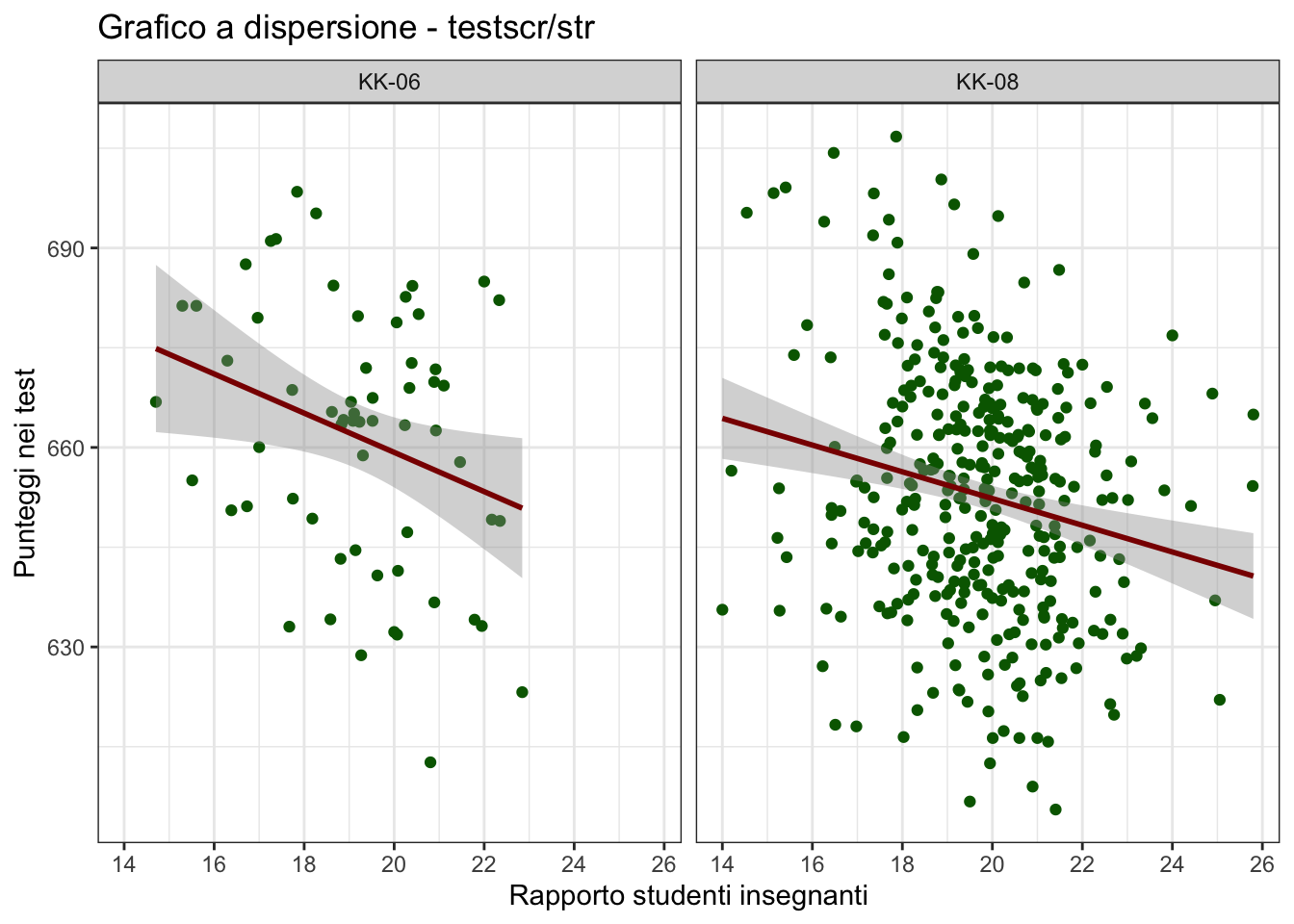
Prime manipolazione di dati usando dplyr
library(dplyr)Calcoliamo la media e la standard deviation di testscr
CASchools |>
summarize(m = mean(testscr), s = sd(testscr)) m s
1 654.1565 19.05335Possiamo anche calcolare la media, la deviazione standard e il numero di osservazioni per il gruppo di scuole che hanno un rapporto studenti insegnanti minore di 20, \(str<20\) e il gruppo di scuole che hanno un rapporto maggiore o uguale a venti (\(str>20\)) usando la funzione group_by seguita dall’indicazione del gruppo (nel nostro caso str<20):
df_1 <- CASchools |>
group_by(str<20) |>
summarize(m = mean(testscr),
s = sd(testscr),
n = n())Il risultato delle manipolazioni è un tibble — un sorta di data.frame più flessibile definito nel pacchetto dplyr.
df_1 può essere a sua volta utilizzato per altri calcoli e si comporta in tutto e per tutto come un normale data.frame.
df_1# A tibble: 2 × 4
`str < 20` m s n
<lgl> <dbl> <dbl> <int>
1 FALSE 650. 17.9 181
2 TRUE 657. 19.4 239I tibble sono una versione migliorata dei tradizionali data.frame, progettata per semplificare l’analisi dei dati in R. Tuttavia, i data.frame sono ancora molto utilizzati e sono l’oggetto dati di base per molti pacchetti in R. Fortunatamente, molti dei comandi di R disegnati per i data.frame funzionano anche per i tibble.
Le maggiori differenze fra i tibble e i data.frame sono:
Tipo di output: Il metodo di visualizzazione di un
tibbleè più compatto e leggibile rispetto a quello di un data.frame.Comportamento dei nomi delle variabili: in un
tibble, i nomi delle variabili sono sempre conservati e non vengono mai modificati (ad esempio, i nomi delle variabili non vengono convertiti in stringhe). In undata.frame, i nomi delle variabili possono essere modificati o convertiti in stringhe.Comportamento di default dei dati mancanti: in un
tibble, i dati mancanti vengono visualizzati in modo più chiaro rispetto a undata.frame.Comportamento della subsetting: in un
tibble, il subsetting (o l’estrazione di sottoinsiemi di dati) è più rigoroso rispetto a undata.frame, in quanto conserva sempre la classe deltibble, anche se viene restituito un singolo valore.Funzioni dplyr: un
tibbleè progettato per essere compatibile con le funzioni del pacchetto dplyr, che sono utilizzate per manipolare i dati.
Abbiamo visto che una stima della differenza dei valori attesi fra i due gruppi \[
\Delta = E(testscr|str<20) - E(testscr|str\geqslant20)
\] può essere ottenuta calcolando la differenza delle medie campionarie dei due gruppi e può essere ottenuta usando le informazioni in df_1:
## Differenza delle medie campionarie
df_1$m[2]-df_1$m[1][1] 7.169435e, quindi, \[ \hat{\Delta} = \overline{testscr}_{str<20} - \overline{testscr}_{str\geqslant20} = 7.1694355. \]
Con le stesse informazioni è possibile calcolare l’intervallo di confidenza al 95% per \(\Delta\) che è dato da \[
\hat{\Delta}\pm1.96\times\sqrt{\frac{s_{str<20}^{2}}{n_{str<20}}+\frac{s_{str\geqslant20}^{2}}{n_{str\geqslant20}}}.
\] Usando le informazioni contenute in df_1 otteniamo: \[
(3.5909173, 10.7479537)
\]
Qualcosa di più complicato
Invece di stimare la variazione del valore atteso rispetto alle due macro-categorie (\(str<20\) e \(str\geqslant20\)) possiamo provare a stimare il valore atteso condizionatamente a piccoli intervalli. Per esempio, possiamo voler stimare la seguente differenza \[ E(testscr|20.1 < str \leqslant 20.6) - E(testscr|20.6 < str \leqslant 21.1) \] oppure \[ E(testscr|21.6 < str \leqslant 22) - E(testscr|22 < str \leqslant 22.5). \]
Per stimare queste quantità utilizzando i dati nel campion, è necessario calcolare la media campionaria per le scuole che hanno un \(str\) che appartiene a ciascun intervallo. Per costruire questi intervalli, possiamo utilizzare la funzione cut(). La funzione cut() è utilizzata per suddividere un vettore numerico in più intervalli.
La sintassi della funzione cut() è la seguente:
cut(x, breaks,
labels = NULL,
include.lowest = FALSE,
right = TRUE,
dig.lab = 3, ...)dove:
xè il vettore numerico da suddividere in binbreaksè un vettore contenente i valori di taglio, ovvero i punti di separazione tra i bin. Questo può essere specificato in diversi modi, ad esempio tramite un numero intero che specifica il numero di bin desiderati o un vettore numerico che specifica i limiti di ogni bin.labelsè un vettore di etichette per ogni bin. Se non specificato, gli intervalli saranno etichettati in base ai loro limiti.include.lowestindica se includere o meno il valore più basso del vettore x nel primo bin. Il valore predefinito è FALSE.rightindica se i bin devono essere chiusi a destra o a sinistra. Il valore predefinito è TRUE, ovvero i bin sono chiusi a destra.dig.labè il numero di cifre decimali da utilizzare per le etichette, se specificato....sono altri argomenti opzionali.
Ecco un esempio di utilizzo della funzione cut() per suddividere str in tre bin di uguale ampiezza:
str_cat3 <- cut(CASchools$str, 3)
summary(str_cat3) (14,17.9] (17.9,21.9] (21.9,25.8]
73 305 42 In questo caso il comando summary produce una tavola di frequenza con il numero delle scuole in ciascuna delle tre categorie (14,17.9], (17.9,21.9], (21.9,25.8].
Possiamo anche specificare i breaks in modo esplicito
str_cat3 <- cut(CASchools$str, c(13,20, 21, 26))
summary(str_cat3)(13,20] (20,21] (21,26]
243 86 91 In questo ultimo caso, gli intervalli sono (13,20], (20,21], (21,26].
str_cat3 e, in generale, l’output di cut è un oggetto di classe factor. Questo tipo di variabili sono utilizzate per rappresentare variabili categoriche o qualitative, ovvero variabili che possono assumere un numero limitato di categorie o livelli (come il numero di intervalli nel nostro questo caso). La funzione summary() restituisce una tavola di frequenza per questo tipo di variabili perchè non avrebbe senso calcolare media, mediana e le altre quantità che sono solitamente restituita da summary quando l’argomento è una variabile di tipo numeric.
library(knitr)
df_2 <- CASchools |>
1 mutate(str_cat = cut(str, 25)) |>
2 group_by(str_cat) |>
3 summarize(m = mean(testscr), s = sd(testscr), n = n())
4df_2 |> kable()- 1
-
la funzione
cutper dividerestrin25intervalli; - 2
-
group_bysuddivideCaschoolin gruppi specificati dastr_cat - 3
-
summarizecalcola la media, la standard deviation e il numero di osservazioni per ciascun gruppo - 4
-
kabblerestituisce la tavole dei valori
| str_cat | m | s | n |
|---|---|---|---|
| (14,14.5] | 646.0500 | 14.778549 | 2 |
| (14.5,14.9] | 681.0750 | 20.117175 | 2 |
| (14.9,15.4] | 669.0583 | 27.490822 | 6 |
| (15.4,15.9] | 666.4300 | 16.397309 | 5 |
| (15.9,16.4] | 657.4625 | 31.451667 | 4 |
| (16.4,16.8] | 656.4000 | 22.941904 | 12 |
| (16.8,17.3] | 655.1200 | 19.810348 | 10 |
| (17.3,17.8] | 661.8417 | 21.060796 | 24 |
| (17.8,18.2] | 660.9820 | 21.377904 | 25 |
| (18.2,18.7] | 655.2611 | 19.005517 | 27 |
| (18.7,19.2] | 659.1279 | 17.430919 | 43 |
| (19.2,19.7] | 654.1674 | 18.195812 | 46 |
| (19.7,20.1] | 652.2074 | 16.740562 | 54 |
| (20.1,20.6] | 652.5538 | 18.840602 | 39 |
| (20.6,21.1] | 650.9581 | 18.103746 | 37 |
| (21.1,21.6] | 645.9219 | 17.020844 | 32 |
| (21.6,22] | 651.4000 | 19.099851 | 15 |
| (22,22.5] | 650.9208 | 14.543983 | 12 |
| (22.5,23] | 639.0750 | 16.285656 | 10 |
| (23,23.4] | 643.8833 | 17.057683 | 6 |
| (23.4,23.9] | 658.9750 | 7.672113 | 2 |
| (23.9,24.4] | 676.8500 | NA | 1 |
| (24.4,24.9] | 651.2000 | NA | 1 |
| (24.9,25.3] | 642.3833 | 23.492246 | 3 |
| (25.3,25.8] | 659.5750 | 7.601398 | 2 |
Alcuni degli errori standard sono uguali a NA perché in almeno uno dei gruppi il numero di osservazioni è inferiore a 2, il numero minimo per poter calcolare questa misura dispersione.
Manipolando df_2, possiamo calcolare le differenze nelle media campionarie fra due intervalli adiacenti.
1df_3 <- df_2 |> mutate(Delta_str = paste0(str_cat, "-", lag(str_cat)),
2 Delta_testscr = m - lag(m),
3 stderr = sqrt(s^2/n + lag(s^2/n))) |>
4 select(Delta_str, Delta_testscr, stderr)
5kable(df_3)- 1
-
la variabile
Delta_strè uguale alla differenza dei due intervalli ottenuta incollandopaste0l’intervallo di ciascuna riga con quella precedente (la funzionelag(m)associa il valore dimdella riga precedente). Questa variabile è utile per annotare l’asse delle ascisse del grafico che produrremo prodotto in seguito. - 2
-
Delta_strcontiene la differenze delle medie campionari di due intervalli successivi. Queste differenze sono calcolate usandom - lag(m)e quindiDelta_testscrè uguale am, la media per l’intervallo, meno il valore della media per l’intervallo che preceda la riga in considerazione (lag(m)) - 3
-
stderrè l’errore standard della differenza delle medie in ciascun intervallo che è uguale a - 4
-
selezioniamo le variabili che ci servono per il grafico mediante la funzione
select() - 5
-
kable(df_3)formatta ildata.framecome una tavolohtml. La funzionekableè contenuta nel pacchettoknitr.
| Delta_str | Delta_testscr | stderr |
|---|---|---|
| (14,14.5]-NA | NA | NA |
| (14.5,14.9]-(14,14.5] | 35.0250092 | 17.650867 |
| (14.9,15.4]-(14.5,14.9] | -12.0166626 | 18.119269 |
| (15.4,15.9]-(14.9,15.4] | -2.6283356 | 13.406413 |
| (15.9,16.4]-(15.4,15.9] | -8.9674973 | 17.351547 |
| (16.4,16.8]-(15.9,16.4] | -1.0625102 | 17.063492 |
| (16.8,17.3]-(16.4,16.8] | -1.2799901 | 9.116244 |
| (17.3,17.8]-(16.8,17.3] | 6.7216634 | 7.597798 |
| (17.8,18.2]-(17.3,17.8] | -0.8596639 | 6.063179 |
| (18.2,18.7]-(17.8,18.2] | -5.7208867 | 5.626609 |
| (18.7,19.2]-(18.2,18.7] | 3.8667929 | 4.521516 |
| (19.2,19.7]-(18.7,19.2] | -4.9605187 | 3.776709 |
| (19.7,20.1]-(19.2,19.7] | -1.9599817 | 3.519560 |
| (20.1,20.6]-(19.7,20.1] | 0.3464398 | 3.780410 |
| (20.6,21.1]-(20.1,20.6] | -1.5957329 | 4.237893 |
| (21.1,21.6]-(20.6,21.1] | -5.0362355 | 4.232186 |
| (21.6,22]-(21.1,21.6] | 5.4781262 | 5.776997 |
| (22,22.5]-(21.6,22] | -0.4791743 | 6.476694 |
| (22.5,23]-(22,22.5] | -11.8458328 | 6.644512 |
| (23,23.4]-(22.5,23] | 4.8083344 | 8.661198 |
| (23.4,23.9]-(23,23.4] | 15.0916901 | 8.827500 |
| (23.9,24.4]-(23.4,23.9] | 17.8749847 | NA |
| (24.4,24.9]-(23.9,24.4] | -25.6499939 | NA |
| (24.9,25.3]-(24.4,24.9] | -8.8166707 | NA |
| (25.3,25.8]-(24.9,25.3] | 17.1916402 | 14.589465 |
Si noti che per prima riga la differenza delle medie è NA. Il motivo è che non c’è un intervallo con valori più piccoli di per poter calcolare la differenza. La seconda riga ci dice che \[
\overline{testscr}_{str \in (14.5,14.9]} - \overline{testscr}_{str \in (14,14.5]} = 35.0250092,
\] e che quindi scuole con classi con \((14.5,14.9]\) studenti per insegnante hanno punteggi più alti di circa 35.0250092 punti rispetto a quelle con \(str\in (14,14.5]\). Questo valore positivo (classi più piccole hanno test score più bassi) e molto grande (quasi due volte la deviazione standard dei punteggi in tutto il campione) è dovuto al fatto che stiamo stimando la differenza dei valori attesi usando soltanto 4 scuole. Un numero troppo esigue per aspettarci che la stima sia in qualche modo “vicina” a quella che potremmo stimare se avessimo a disposizione i dati nel campione.
La terza riga ci dice che \[ \overline{testscr}_{str \in (14.9,15.4]} - \overline{testscr}_{str \in (14.5,14.9]} = -12.0166626, \] e che quindi scuole con \(str\in (14.9,15.4]\) hanno punteggi più alti di circa -12.0166626 punti rispetto a quelle con \(str\in (14.5,14.9]\). E così via per le altre righe.
E’ molto probabile che tutte le stime e non soltanto quelle della prima riga siano particolarmente imprecise visto che sono tutte basate su un numero esiguo di osservazioni. Per quantificare la loro precisione, o la loro imprecisione, possiamo costruire l’intervallo di confidenza (al 95%) per ciascun valore dell’intervallo di \(str\). L’intervallo di confidenza al 95% è:
c(df_3$Delta_testscr - 1.96 * df_3$stderr,
df_3$Delta_testscr + 1.96 * df_3$stderr)dove stderr è l’errore standard della differenza delle media che è stato calcolato nel precdedente blocco di codice.
Per aggiungere l’intervallo di confidenza a df_3 possiamo usare dplyr e la funzione mutate:
df_3 <- df_3 |>
1 mutate(ci_sx = Delta_testscr - 1.96 * stderr,
2 ci_dx = Delta_testscr + 1.96 * stderr)
kable(df_3)- 1
- l’estremo sinistro dell’intervallo di confidenza;
- 2
- l’estremo destro dell’intervallo di confidenza;
| Delta_str | Delta_testscr | stderr | ci_sx | ci_dx |
|---|---|---|---|---|
| (14,14.5]-NA | NA | NA | NA | NA |
| (14.5,14.9]-(14,14.5] | 35.0250092 | 17.650867 | 0.4293091 | 69.620709 |
| (14.9,15.4]-(14.5,14.9] | -12.0166626 | 18.119269 | -47.5304300 | 23.497105 |
| (15.4,15.9]-(14.9,15.4] | -2.6283356 | 13.406413 | -28.9049041 | 23.648233 |
| (15.9,16.4]-(15.4,15.9] | -8.9674973 | 17.351547 | -42.9765294 | 25.041535 |
| (16.4,16.8]-(15.9,16.4] | -1.0625102 | 17.063492 | -34.5069539 | 32.381934 |
| (16.8,17.3]-(16.4,16.8] | -1.2799901 | 9.116244 | -19.1478280 | 16.587848 |
| (17.3,17.8]-(16.8,17.3] | 6.7216634 | 7.597798 | -8.1700207 | 21.613347 |
| (17.8,18.2]-(17.3,17.8] | -0.8596639 | 6.063179 | -12.7434947 | 11.024167 |
| (18.2,18.7]-(17.8,18.2] | -5.7208867 | 5.626609 | -16.7490402 | 5.307267 |
| (18.7,19.2]-(18.2,18.7] | 3.8667929 | 4.521516 | -4.9953795 | 12.728965 |
| (19.2,19.7]-(18.7,19.2] | -4.9605187 | 3.776709 | -12.3628686 | 2.441831 |
| (19.7,20.1]-(19.2,19.7] | -1.9599817 | 3.519560 | -8.8583199 | 4.938356 |
| (20.1,20.6]-(19.7,20.1] | 0.3464398 | 3.780410 | -7.0631636 | 7.756043 |
| (20.6,21.1]-(20.1,20.6] | -1.5957329 | 4.237893 | -9.9020039 | 6.710538 |
| (21.1,21.6]-(20.6,21.1] | -5.0362355 | 4.232186 | -13.3313205 | 3.258850 |
| (21.6,22]-(21.1,21.6] | 5.4781262 | 5.776997 | -5.8447884 | 16.801041 |
| (22,22.5]-(21.6,22] | -0.4791743 | 6.476694 | -13.1734956 | 12.215147 |
| (22.5,23]-(22,22.5] | -11.8458328 | 6.644512 | -24.8690769 | 1.177411 |
| (23,23.4]-(22.5,23] | 4.8083344 | 8.661198 | -12.1676134 | 21.784282 |
| (23.4,23.9]-(23,23.4] | 15.0916901 | 8.827500 | -2.2102091 | 32.393589 |
| (23.9,24.4]-(23.4,23.9] | 17.8749847 | NA | NA | NA |
| (24.4,24.9]-(23.9,24.4] | -25.6499939 | NA | NA | NA |
| (24.9,25.3]-(24.4,24.9] | -8.8166707 | NA | NA | NA |
| (25.3,25.8]-(24.9,25.3] | 17.1916402 | 14.589465 | -11.4037118 | 45.786992 |
Come si vede chiaramente dall’analisi della tabella, tutti gli intervalli di confidenza sono molto ampi. Come preannunciato, i dati a nostra disposizione non sono abbastanza informativi per poter stimare tutte le differenze su intervalli così poco numerosi. Anche nel caso in cui considerassimo la differenza delle medie in scuole con \(str\in(18.7,19.2]\) (27 scuole) e scuole con \(str\in (18.2,18.7]\) (47 scuole), l’intervallo di confidenza è molto ampio: \((-4.9953795, 12.7289653)\). Un intervallo di confidenza così ampio implica che non possiamo neanche quantificare con l’appropriata confidenza il segno della differenza che potrebbe essere -12 o 2.
La rappresentazione grafica delle informazioni contenute in una tavole facilita spesso la comprensione dei risultati.
1ggplot(df_3, aes(x=Delta_str,y=Delta_testscr)) +
2 geom_pointrange(aes(ymin=ci_sx, ymax=ci_dx)) +
3 geom_hline(yintercept = 0, col = "darkred") +
theme_bw() +
xlab("Intervalli str") + ylab("Delta Media testscr") +
4 theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))- 1
- sull’ascissa abbiamo la differenza degli intervalli, sull’ordinata la differenza delle medie;
- 2
-
la geometria utilizzata è
geom_pointrange, che “plotta” la differenza delle medie (il punto) e l’intervallo di confidenza al 95% definito da ((ci_sx, ci_dx)) e rappresentato dalle linee che si estendono verticalmente. - 3
-
geom_hline(yintercept=0, col = "darkred")produce una riga orizzonate di colore rosso scuro - 4
-
le etichette dell’asse della
xsono ruotate di 90 gradi per favorire la loro leggibilità.
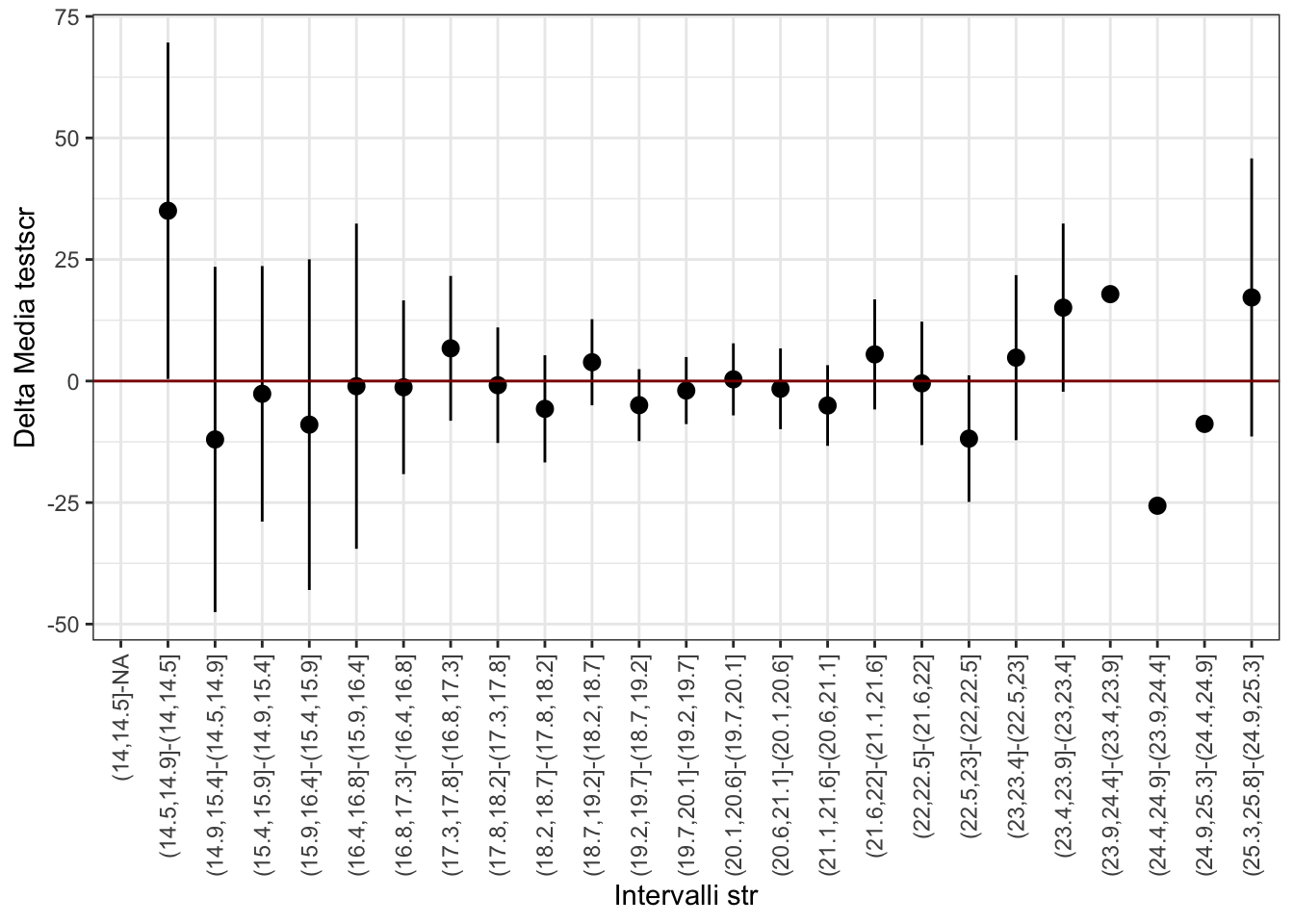
Il grafico mostra che la stima di molte delle differenze è negativa e che gli intervalli di confidenza (eccettuati i tre casi in cui non è possibile costruire l’intervallo di confidenza) sono troppo ampi per poter concludere che il valore della differenza nella popolazione sia negativa